of inverse Fourier transformation.
In order to generate fBm spectral density function S(f) (c.f. [9]) of
these coefficients must be proportional to 
Spectral synthesis (also called Fourier transform filtering) is another representative of how fBm surface can be obtained [1].
First step we compute the complex coefficients of inverse Fourier transformation.
In order to generate fBm spectral density function S(f) (c.f. [9]) of
these coefficients must be proportional to
where 
controls the fractal dimension of the final object according to
and H denotes Hurst exponent. Then we calculate the inverse Fourier transformation in two dimensions according to formula
The function f(x,y) is then fBm with its fractal dimension
The coefficients of Fourier transformation with lowest indices have the biggest influence to resulting shape of the surface (see in Figure 4) and the higher indices manifest themselves just locally.
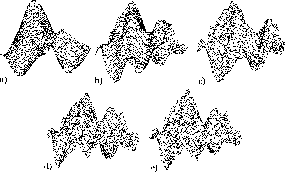
Figure: Surfaces obtained with the spectral synthesis using a) 2, b) 4, c) 8,
d) 16 and e) 32 respectively members of Fourier series.