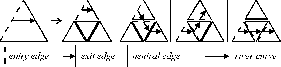
Figure 5: Production for generating the river curve in Bacus-Naur form. Arrows signify the direction of river curve.
Prusinkiewicz and Hammel [11] use context sensitive rewriting processes based on a random midpoint displacement method [9] on a triangular grid. Their method creates one non-branching river as result of context sensitive L-system [12] operating on a set of triangles.

Figure 5: Production for generating the river curve in Bacus-Naur form. Arrows signify the direction of river curve.
The productions for generating model of river contain two types
of triangles: ![]() and
and ![]() . Triangles
. Triangles ![]() differ from
differ from ![]() in such a way that
through
in such a way that
through ![]() goes a river. The edges of
goes a river. The edges of ![]() are labeled entry ,exit and neutral .
The production predecessor is just triangle
are labeled entry ,exit and neutral .
The production predecessor is just triangle ![]() . Each production subdivides the triangle into four
smaller triangles and includes the following constrains (see Figure 5):
. Each production subdivides the triangle into four
smaller triangles and includes the following constrains (see Figure 5):
The predecessor and the successor can be rotated, reflected and scaled before every application. The construction of the river starts from the triangle having one entry, one exit, and one neutral edge. The rewriting process is repeated recursively until required level of detail is reached. We can see in the Figure 6 how this method works.
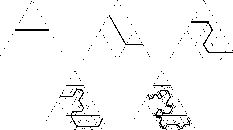
Figure 6: Course of generating river.