Techniques such as Fourier filtering [1, 9], random midpoint displacement [4], Poisson faulting [6] often creates more or less realistic fractal forgeries of nature. They do not consider over that the real terrain is not self-similar or identical from top to bottom. In thus generated terrains we do not find craters, streaks, and other features typical for "extraterrestrial terrain".
Pickover [10] uses a logistic function (2) for simulating these features.
This function was originally introduced by Belgian sociologist and
mathematician P.F. Verhulst to model the growth of population limited by finite resources. If
, the 
are "random" numbers from the interval (0,1) with U-shaped probability
distribution (see Figure 7 a) ).
Using transformation of the 
according to
we can thought as random number generator with the numbers uniformly
distributed over the interval (0,1) (see Figure 7 a)).
Pickover [10] recommended another transformation given by
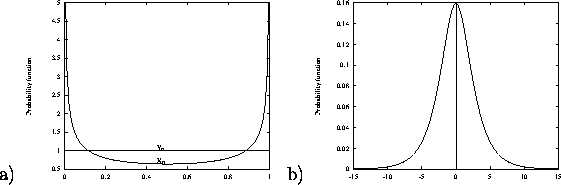
Figure 7: a) Distribution of and b) Distribution of 
This transformation may operate on the logistic variable and Collins et al. [2]
shows that the transformation (4) generates a sequence of "random" numbers with a
near-Gaussian distribution (see Figure 7 b) ). In the next step we extend
equations (3) and (4) to 3 dimensions. We assume
distribution to be a radius and denotes an angle
Variables u and v in equation (5) are thus coordinates of and in polar coordinate system. In every iteration the u and v coordinates are evaluated and an element P(u,v) in 2D array is
incremented by one. After many iterations array P(u,v) viewed as 3D surface resembles a circular ridge with center at 
. Each ridge has a near Gaussian cross-section. The diameter of the crater is controlled by variable 
i.e. the distance from center to the ridge.
Advantage of this method is that it can be used for tuning of already created terrains. The near-Gaussian numbers are easy to incorporate into software for stochastic modeling and produce structures that look like a crater with self-similar details.
