We cover our raster image with regular grid of sample points (vertices of triangular meshes). In individual points we determine third coordinate according to the specific value of image function.
However, eventual triangular meshes are still too rough. Therefore we smooth triangles according to the edges detected
in raster image (as shown in Fig. 2).
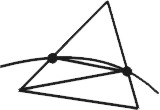
Simple object and its final relief are shown in Fig. 3.
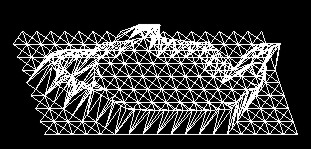
To avoid disadvantages of previous approach, we use edge tracing to create adaptive meshes along the edges (Fig. 4).
If there is more than one object in the image or if this object contains other inner shapes, first we find all individual cyclic curves and then apply following procedure for each of them.
Let us suppose that input edge is represented by the list of its points and is of 1 pixel length, i.e. each point has exactly two adjacent ones.
Method:
In the end we triangulate eventual area of the polygon to get continuous triangular meshes.
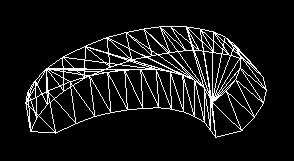
To recognize shapes in the raster image the edges of objects are very important. That is why we tried to create relief not of whole object area but of edges only (see Fig. 5).
The best solution is negative relief because the valley created in such way allows user to follow easily the edge and not to lose haptic contact.
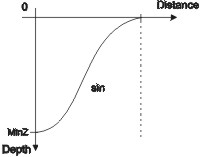
The edge itself is located in the lowest level of the relief. The depth coordiate of surrounding points should come near to it along some continuous curve to reach good haptic feeling. We used sine function to interpolate coordinates (Fig. 6).
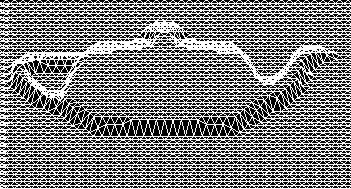
The negative edge must be of certain length for user to recognize it. The edges of very narrow objects cannot be well distinguishable and can be merged into one negative area. We can use scaling to zoom details and get better notion of image. Negative edge is also useful for visualization of graphs of math functions. In raster images language graph is a curve consisting of discrete function values. We examined this approach for functions with smooth continuous graph like sine (Fig. 7). Picture on the right shows how is this relief influenced by changing function argument (from x to 2x).
Following method is possible to apply to any general raster image. However, the results of recognition of image content are not as conclusive as applying to simple objects. The information available to get depth coordinate is the image function again. The x and y coordinate of each pixel is known, accordingly we try to replace its brightness by corresponding height. In case of colour raster image we used the RGB (Red-Green-Blue) colour model where we added up the individual colour components. Then the z coordinate increases from black [0.0,0.0,0.0] to white [1.0,1.0,1.0], black is the lowest level of relief.
The smoothing of adjoining triangles is very important for acceptable haptic feeling. But, as shown in Fig. 9, if we smooth out the sharp transition edges we lose some information about the edges of objects and reduce the probability to recognize object.
