Next: Fast Fourier transformation
Up: paper
Previous: Abstract
In image processing it is a fundamental problem how to reconstruct
features (like the original gradients) from sampled data. A
typical example is the reconstruction of medical data obtained as
CT or MRI scans. The data can be sampled at regular or irregular
grids points. If we use direct volume rendering to visualize such
a data set staircase artifacts can occur. In case of binary
segmented data the staircase aliasing is stronger than in case of
gray-scale data, where the gradients can be estimated more
accurately. A binary volume can be obtained as a result of a
segmentation. The segmented data cannot be rendered directly,
because the result looks like built from Lego pieces. Therefore,
various preprocessing techniques are used to eliminate this
aliasing. The classical method is convolution-based filtering.
Convolution-based methods have mostly local influence, because of
the limited support of the kernel function. Although filtering
with a wide kernel causes dependency on wider neighborhood, it is
rather time-consuming and removes fine details. There are several
approaches for solving this problem. One research direction is
interpolation oriented assuming, that accurate samples are
available. The sinc and cosc functions are considered as ideal
interpolation and derivative filters respectively. These
derivative reconstruction techniques based on windowing are local
methods as for practical reasons only a limited number of
neighboring samples are taken into account. Another approach for
derivative reconstruction is approximation oriented. Here it is
assumed, that the sampled function is noisy, which is typical,
when some real physical properties are measured. The basic idea is
to estimate the inclination or the normal from a larger
neighborhood. In order to reduce staircase aliasing, several
methods were proposed for normal computation especially in binary
volumes. Contextual shading techniques try to fit locally
approximated plane or a biquadratic functions to the set of points
that belong to the same iso-surface. These methods are time
consuming and limited to a certain neighborhood. A rather new
research direction is based on a gradient estimation using 3D
distance maps.
The new method we have implemented, designed by
Neumann et al. [4] is a general tool for filtering
binary and gray-scale data sets. Figure 1 illustrates
this filtering technique on a CT scan of a human body.
Figure 1:
Direct volume rendering of a human body using the original (a)
and the filtered (S = 1, G = 1) data (b).
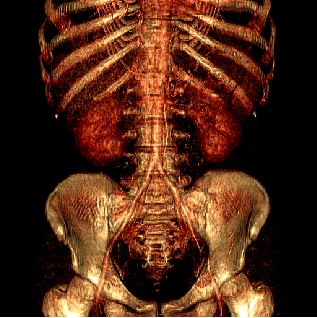
| 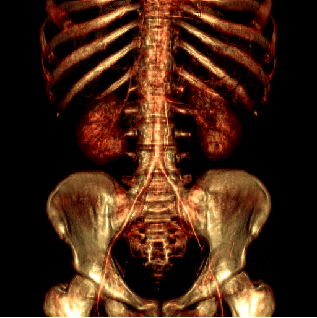 |
| (a) | (b) |
Similarly to the distance maps, generated from binary volumes,
this filtering technique creates a smooth volume from gray-scale
data. Unlike convolution based filtering, the smoothing effect is
global due to a global curvature minimization. Feature
preservation is the main characteristic of this novel filtering
approach. By globally penalizing large gradient deviations,
important features and fine details like edges or iso-surfaces are
preserved. The method is based on a quadratic penalty function
 .
.  is defined so that feature preservation and smoothing is
simultaneously possible. Therefore
is defined so that feature preservation and smoothing is
simultaneously possible. Therefore 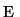 consists of the following
three components summed over every sample point
consists of the following
three components summed over every sample point 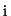 :
:
- difference squared between filtered value
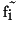 and
original value
and
original value 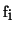
- difference squared between the gradient of the filtered value
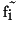 and the original value
and the original value 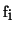
- the squared curvature of the filtered function
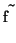
The 1D case of the penalty function 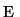 has the following
structure:
has the following
structure:
![\begin{displaymath}
E=\sum_{i}[(\tilde{f}_{i}-f_{i})^{2}+G\cdot[(\tilde{f}_{i+1...
...\cdot(\tilde{f}_{i+1}+\tilde{f}_{i-1}-2
\tilde{f}_{i})^{2}].
\end{displaymath}](img8.gif) |
(1) |
The weights 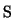 and
and 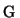 determine the relative importance of
feature preservation as opposed to smoothing. At the minimum
location of the penalty function
determine the relative importance of
feature preservation as opposed to smoothing. At the minimum
location of the penalty function 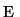 the partial derivatives
according to all the
the partial derivatives
according to all the 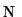 unknown values
unknown values 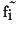 have to be
equal to zero, where i = 0, 1, 2, ..., N-1:
have to be
equal to zero, where i = 0, 1, 2, ..., N-1:
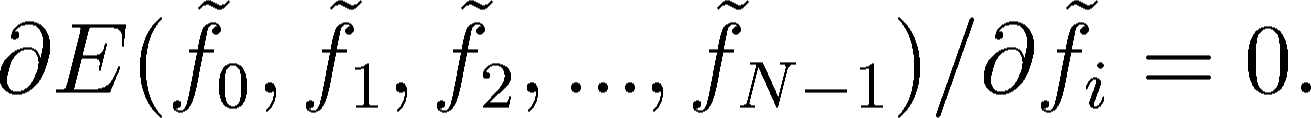 |
(2) |
As penalty function  is a quadratic function, the partial
derivatives are linear functions of variables
is a quadratic function, the partial
derivatives are linear functions of variables 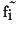 .
Therefore, having all of these partial derivatives evaluated, a
large linear equation system is obtained with
.
Therefore, having all of these partial derivatives evaluated, a
large linear equation system is obtained with 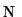 unknown
variables:
unknown
variables:
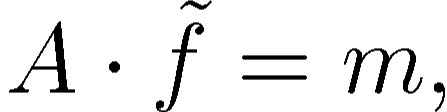 |
(3) |
where 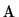 is a sparse coefficient matrix, and
is a sparse coefficient matrix, and 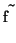 is the
unknown vector containing the
is the
unknown vector containing the 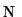 samples of the filtered
function. Vector
samples of the filtered
function. Vector 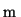 is derived from the original function samples
is derived from the original function samples
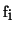 in the following way:
in the following way:
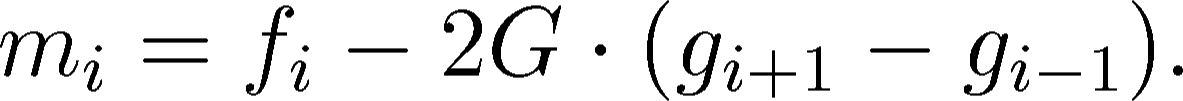 |
(4) |
Matrix 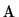 , derived from the partial derivatives, is a band matrix
defined by a symmetric point spread vector
, derived from the partial derivatives, is a band matrix
defined by a symmetric point spread vector 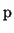 :
:
![\begin{displaymath}
p = [p_1,p_2,p_3,p_4,p_5] = [S-G, -4S, 1 + 6S + 2G, -4S, S-G],
\end{displaymath}](img20.gif) |
(5) |
In fact, the multiplication of 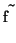 with coefficient matrix
with coefficient matrix
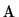 is a convolution of the unknown vector
is a convolution of the unknown vector 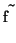 with kernel
with kernel
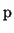 . Therefore, it is not necessary to use any computationally
expensive linear algebra method, since a simple deconvolution
leads to the solution. Such a deconvolution can be efficiently
performed in frequency domain.
Using fast Fourier transformation, the filtering algorithm
consists of the following steps:
. Therefore, it is not necessary to use any computationally
expensive linear algebra method, since a simple deconvolution
leads to the solution. Such a deconvolution can be efficiently
performed in frequency domain.
Using fast Fourier transformation, the filtering algorithm
consists of the following steps:
- estimation of gradients
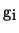 using linear regression
using linear regression
- non-linear operations on the gradient function
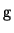
- calculation of function
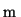 using the modified
using the modified 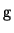
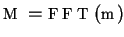 - Fourier transformation of function
- Fourier transformation of function 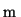
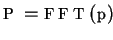 - Fourier transformation of function
- Fourier transformation of function 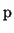
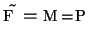 - deconvolution in frequency domain
- deconvolution in frequency domain
-
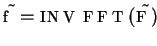 - inverse Fourier
transformation of
- inverse Fourier
transformation of 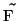
Ivan Viola, Matej Mlejnek
2001-03-22




![\begin{displaymath}
A = \left[
\begin{array}{cccccccc}
p_3 & p_4 & p_5 & 0 & ...
...\\
0 & 0 & 0 & 0 & p_1 & p_2 & p_3 &
\end{array}
\right].
\end{displaymath}](img21.gif)