Fast Fourier transformation

Fourier transformation is a tool which generates the spectrum of a signal yielding a frequency-domain representation. Since this transformation is unambiguous the original signal can be reconstructed from its spectrum by an inverse transformation. The Fourier transform 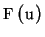$F(u)$ of a 1D function 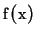$f(x)$ is defined as:

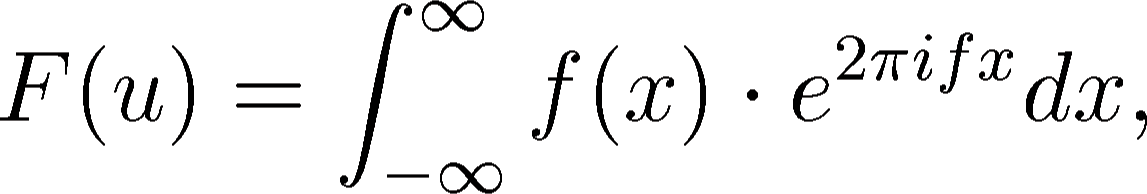$$F(u)=\int_{-\infty }^{\infty }f(x)\cdot e^{2\pi ifx}dx,$$ (6)

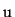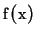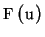where $u$ is a value in the frequency domain. The inverse Fourier transformation for reconstructing $f(x)$ from $F(u)$ is defined as:

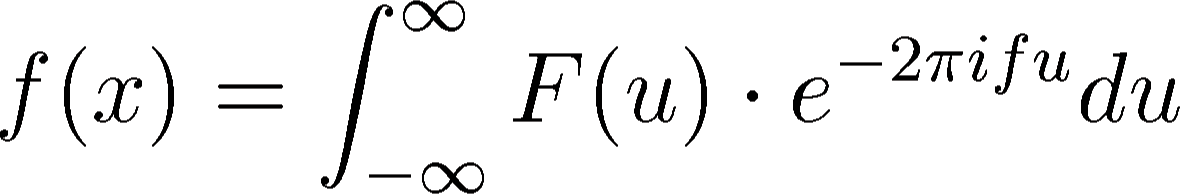$$f(x)=\int_{-\infty }^{\infty }F(u)\cdot e^{-2\pi ifu}du$$ (7)

which is rather similar, except that the exponential term has the opposite sign. In the 3D case, the Fourier transform of a function 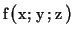$f(x,y,z)$ is defined as follows:

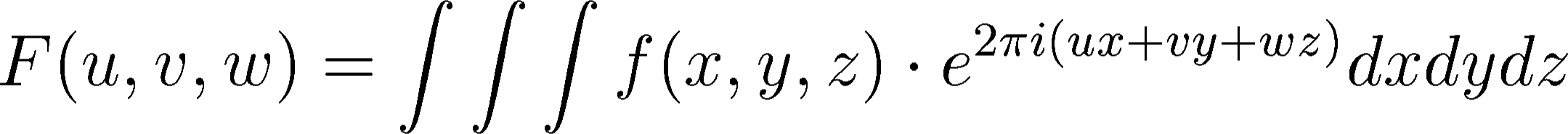$$F(u,v,w)=\int \int \int f(x,y,z)\cdot e^{2\pi i(ux+vy+wz)}dxdydz$$ (8)

The inverse transformation is analogous to the 1D case.