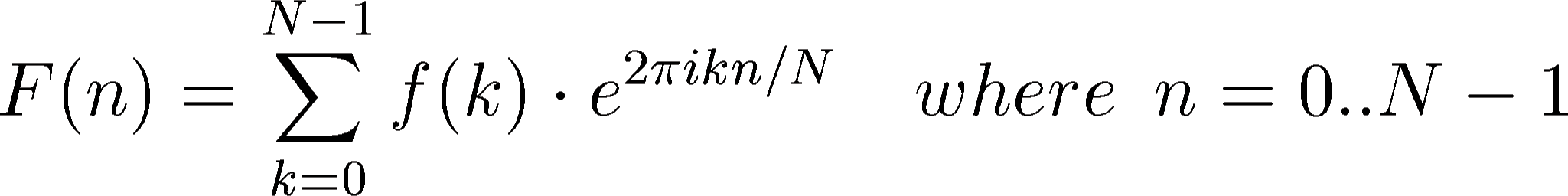Next: Motivation of various implementations
Up: Fast Fourier transformation
Previous: Fast Fourier transformation
But the images are digitized, therefore we need a discrete formulation of the Fourier
transformation, which takes regularly spaced data values, and
returns the coefficients of the discrete Fourier transformation as
a set of equally spaced values in the frequency space. This is
done by replacing the integral by a summation defining
the discrete Fourier transformation (DFT). In 1D, it is
convenient to assume, that the series outside the range 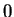 ,
, 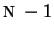 is extended
is extended 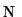 -periodic, thus
-periodic, thus 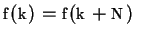 for all
for all 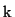 . The
DFT of this series is denoted by
. The
DFT of this series is denoted by 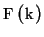 and represented by
and represented by 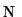 samples. The DFT is defined as follows:
samples. The DFT is defined as follows:
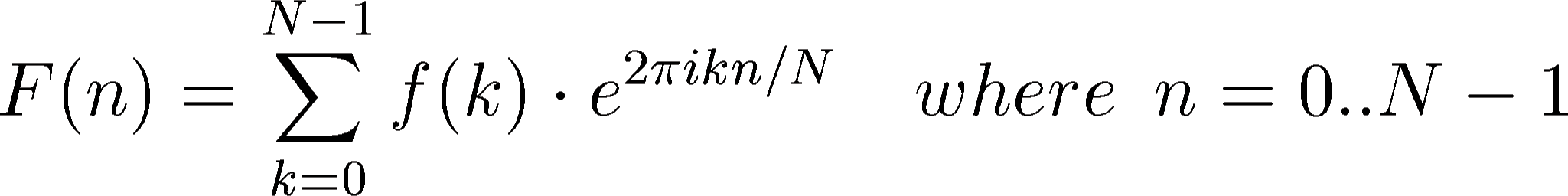 |
(9) |
while the inverse DFT is:
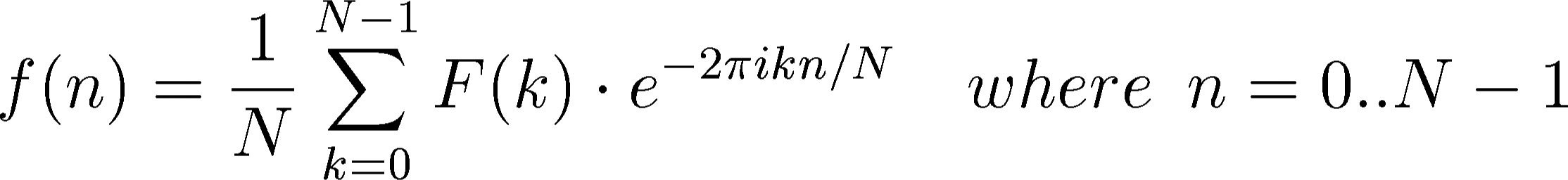 |
(10) |
The 3D DFT is defined by
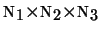 samples in the
frequency domain:
samples in the
frequency domain:
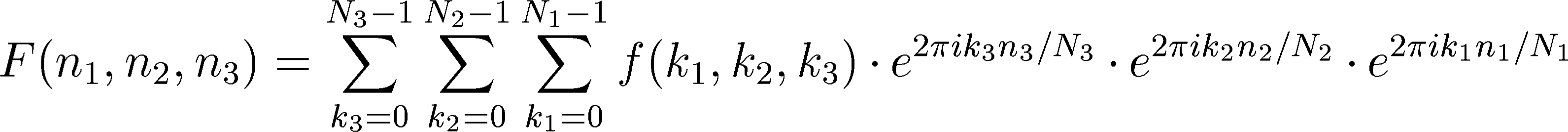 |
(11) |
The inverse transformation is analogous to the 1D case:
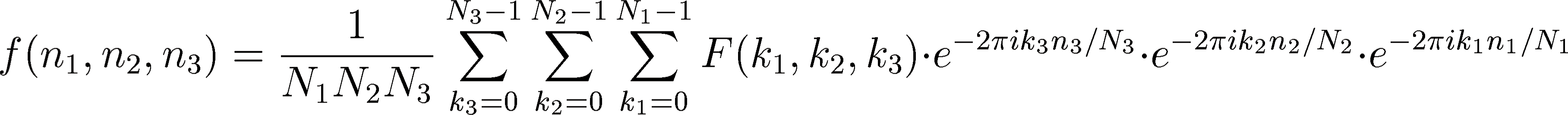 |
(12) |
The DFT can be applied to any complex series.
The computational time is proportional to the square of the number
of points in the series. Instead of the naiv implementation a much
faster algorithm can be used, called FFT (Fast Fourier Transformation)
[2]. DFT requires at least 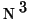 multiplications to
generate all
multiplications to
generate all 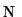 of the coefficients
of the coefficients 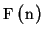 . As it is explained in
[5], the summation can be broken into two parts, one over the
even-numbered elements (k=0,2,4,...) and the other over the odd-numbered
elements (k=1,3,5,...). In turn, each one of these parts can be
broken into its even-numbered and odd-numbered parts, and the
process can be continued, with careful book-keeping, until the
summation has become divided into 1-point Fourier transforms
(which are identity transforms). This repeated dissection of the
series into even- and odd-numbered parts can be implemented by
reversing the bit-pattern of the addresses of the data elements.
After this is done, the required
. As it is explained in
[5], the summation can be broken into two parts, one over the
even-numbered elements (k=0,2,4,...) and the other over the odd-numbered
elements (k=1,3,5,...). In turn, each one of these parts can be
broken into its even-numbered and odd-numbered parts, and the
process can be continued, with careful book-keeping, until the
summation has become divided into 1-point Fourier transforms
(which are identity transforms). This repeated dissection of the
series into even- and odd-numbered parts can be implemented by
reversing the bit-pattern of the addresses of the data elements.
After this is done, the required 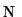 values of
values of 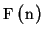 can be
generated by making a sequence of 2,4,8,...-point summations.
Here the number of points in the series is assumed to be a power of
2. Therefore we arrange always our data sets in the middle of
can be
generated by making a sequence of 2,4,8,...-point summations.
Here the number of points in the series is assumed to be a power of
2. Therefore we arrange always our data sets in the middle of
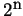 zero pad. The complexity of the algorithm is
zero pad. The complexity of the algorithm is
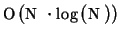 . For example, a transformation of
. For example, a transformation of 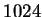 points using the
DFT takes
points using the
DFT takes 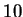 times longer than using the FFT. Note that in
practice comparing speeds of various FFT routines is problematic.
Many of the reported timings have more to do with specific coding
methods and their relationship to the hardware and operating
system. Usually the signal to be digitized is appropriately
filtered before sampling to remove higher frequency components. If
the sampling frequency is not high enough the high frequency
components wrap around and appear in other locations in the
discrete spectrum.
Therefore we have to rearrange our data set after every Fourier
transformation. This can be done by dividing the volume data into
eight parts (similar to the octree subdivision) numbering them and
storing them in the reverse order. The 2D case is sketched on the
figure 2.
times longer than using the FFT. Note that in
practice comparing speeds of various FFT routines is problematic.
Many of the reported timings have more to do with specific coding
methods and their relationship to the hardware and operating
system. Usually the signal to be digitized is appropriately
filtered before sampling to remove higher frequency components. If
the sampling frequency is not high enough the high frequency
components wrap around and appear in other locations in the
discrete spectrum.
Therefore we have to rearrange our data set after every Fourier
transformation. This can be done by dividing the volume data into
eight parts (similar to the octree subdivision) numbering them and
storing them in the reverse order. The 2D case is sketched on the
figure 2.
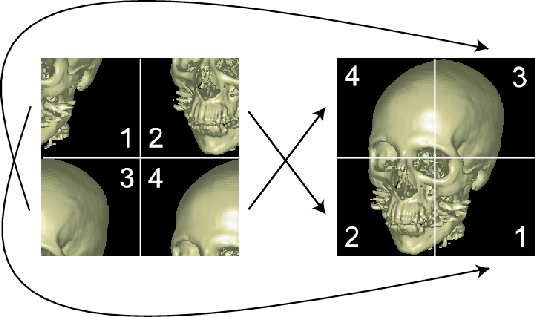
Figure 2:
Wrap around effect: the high frequency
components wrap around and appear in other locations of the
discrete spectrum. This can be solved by rearranging the different
parts.
 |
The Fourier transformation is designed only for periodic signals.
In image processing one might need to analyze non-periodic signals
as well. Then the whole signal (e.g. row of pixels) is considered
as only one period of the signal. This may cause that the values
at the end of the period are influenced by values from the
beginning. If we take a picture as an example, this means, there
will be some artifacts at the border. One effective solution is
the use of zero-padding.
Ivan Viola, Matej Mlejnek
2001-03-22