Simplification Algorithms

In the following some algorithms for polygon mesh simplification are discussed. Quite more algorithms exist than can be mentioned here and, hence, some important and recent algorithms had been chosen [5]. Simplification algorithms can be divided into two classes:

View-independent:

The simplification is not dependent on the spectator's position and viewing angle and need not to be recalculated if the spectator moves. The spectator can not be included into the simplification process causing that invisible or far parts of the scene can not be considered differently than near parts.

View-dependent:

The simplification considers the spectator's position and viewing angle and has to be partially or fully recalculated if the spectator moves. The advantage of view-dependent algorithms is that invisible or far parts of the scene can be simplified more than near parts. This sometimes increases the visual quality of the result incredibly.

The classification of simplification algorithms by quality appears to be as difficult as the simplification problem itself, because subject impressions of the spectator rarely can be described quantitatively. Jerky moving faces or points disturb the human eye very strongly even if the mortion is quite small. Further, the human eye is very sensitive to discontinuities of the silhouette although a more coarse structuring inside the model is noticed less strongly. Some algorithms already provide ways to consider these specialities of the human perception.

Triangle Decimation

Triangle Decimation is one of the first simplification algorithms [8]. It was mainly developed for simplifying the results of the Marching Cubes algorithm for iso-surface extraction from volume data. The Marching Cubes algorithm often produces too fine triangulated polygon meshes with many coplanar faces. This fact implies that a following triangle decimation seems reasonable. The Triangle decimation algorithm considers all vertices during some passes. Each pass will delete a vertex, if this does not change the local topology in the neighborhood and the difference of the original mesh and the resulting mesh is not more than an user definable distance. All triangles containing this vertex are deleted and the hole is re-triangulated. The Triangle Decimation algorithm has the noticeable property not to create new vertices. This property simplifies the reuse of surface normals and texture coordinates, but limits the simplification, because stronger simplification sometimes require the displacement of vertices and/or changing topology. The algorithm can process non-manifold meshes, but does not try to simplify these (non-manifold) parts.

Re-Tiling Polygonal Surfaces

This method is well applicable for smooth, curved surfaces without sharp edges like organic models [10]. The algorithm starts by distributing an user defined number of vertices onto the polygon mesh. Afterwards repulsion forces between these vertices are simulated, causing that the vertices become almost equally distributed (vertices are only allowed to move on the surface). Now, mutual tesselation creates a surface consisting of old and new vertices. A local triangulation improves the aspect ratio of the triangles. Finally, the original vertices are decimated from the surface to obtain a re-tiled model with the new vertices.

Multi-Resolution 3D-Approximations for Rendering Complex Scenes

[7] describes a vertex-clustering algorithm which neither requires nor preserves valid topology. The algorithm is well suited for degenerated or messy models (e.g. hand-drawn CAD models). Most simplification algorithms rarely produce good results for such models or do not work at all.

  

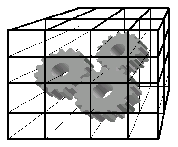
Figure 3: Vertex Clustering

The algorithm starts with assigning each vertex a weight. Vertices of large triangles get larger weights and vertices of smaller appropriate smaller ones. The model's curvature at a vertex is considered with the inverse of the maximum angle between all edge pairs of this vertex. Then a three-dimensional grid divides the scene in many equally sized cells (Figure 3). All vertices inside a cell are clustered to one representative vertex, which is determined from the pre-caclulated weights. The quality of the simplification can be determined by the resolution of the grid. The algorithm is very stable and one of the fastest of its class, but has some disadvantages. Because topology is not preserved and no explicit error bounds in relation to the model exist, the result can be visually less satisfying than the result of slower algorithms. Additionally the result depends on the orientation of the grid and identical objects with different orientations are simplified differently.

Simplification Envelopes

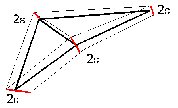
Simplification Envelopes are a method for reliable preservation of local and global topology [1]. The Simplification Envelope of a surface consists of two offset surfaces, which are not more than an user defined 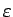$\varepsilon$ distant from the original surface. The outer offset surface is created by a displacement along the normal vector by 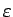$\varepsilon$ and the inner offset surface is created by displacing by 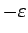$-\varepsilon$ (Figure 4). The envelopes are not allowed to self-intersect, which can be avoided by local reduction of 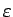$\varepsilon$ (numerical more stable) or analytical calculation (computational expense) and correction of the self-intersection.

  

Figure 4: Simplification Envelopes

Simplification Envelopes achieve very good visual quality, because the simplified model can not be more distant than 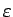$\varepsilon$. This big advantage is also the biggest disadvantage, because drastic simplification often requires the change of topology. Further, algorithms for the calculation of Simplification Envelopes are tricky and difficult in programming. This makes robust systems based on Simplification Evelopes difficult.

Progressive Meshes

Progressive Meshes are a representation of polygon meshes based on edge collapses and vertex splits and a topology-preserving simplification algorithm for the creation of Progressive Meshes itself [3]. A Progressive Mesh consist of a simple base mesh, which was conducted by consecutive edge collapses from the original mesh. A series of vertex splits (inverse operation to edge collapse) creates stepwise more accurate models until the original model is reached, if all vertex splits have beeen executed. The edge collapse and vertex splits can be used for a continous changing between different simplification levels, because they can be executed very quickly. Further it is possible to interpolate the edge collapse and vertex splits to achieve softer transitions (geomorphing).

  

Figure 5: Progressive Meshes

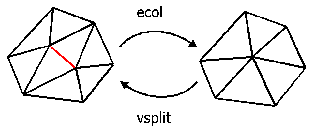The quality of Progressive Meshes depends strongly on the order of the ecol bzw. vsplit operations (Figure 5). Hoppe describes a very accurate and expense algorithm for creating the order of the edge collapses. The method models the approximation error as an explicit energy function, which is minimized. The influence of all edge collapses on the energy function is determined and sorted into a queue. The edge, which minimizes the energy function by the largest amount, is removed from the queue. This changes the influence of edge collapses close to this edge and therefore these edges are recalculated and inserted correctly into the queue. This continues until no further simplification due to topological constraints is possible or an user defined threshold is exceeded.