Hierarchical Dynamic Simplification

Hierarchical Dynamic Simplification (HDS) uses a Vertex Tree, which is continually queried to generate a simplified scene [6]. The Vertex Tree contains only information about the vertices and triangles of the scene. Manifold topology is not required and is not preserved. The Vertex Tree is built hierarchically and each node contains one or more vertices.. The model is simplified by clustering all vertices inside a node to one single representative vertex. Degenerated triangles are removed from the scene and reduce the number of triangles to display. Reversely the representative vertex will be split into the vertices of its child nodes if the node is expanded. This forces some triangles, which have been removed during collapsing, to re-appear and increases the number of triangles to display. One possibility to control simplification is to consider the projected size of each node on the picture plane. While the spectator moves through the scene all nodes which become smaller than an user defined threshold are collapsed. Similar, nodes which exceed the threshold are expanded. Each frame several node collapses and expansions are necessary; this requires a effective data structure containing the information which triangles must be removed from the scene respectively which triangles must be added.

Active Triangle List

The Active Triangle List contains all triangles, which have to be rendered for the current level of simplification. If the spectator moves through the scene, triangles must be continually added and removed from the Active Triangle List. This implementation uses a doubly linked list, which is able to insert and remove elements in constant time. To remove a certain triangle quickly from the Active Triangle List, the position (pointer) of the triangle is stored. The triangles itself are represented by the following structure. Corners contains the vertices of the original model and proxies the vertices of the current simplification.

struct Tri {
    Node*   corners[3];
    Node*   proxies[3];
}

Vertex Tree

The Vertex Tree is generated during a preprocessing stage and controls the order of collapsing and expanding the nodes (Figure 6). Further all necessary informations for the collapsing and expanding of nodes are stored in the Vertex Tree to allow fast access to them.

  

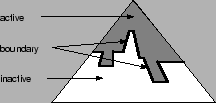
Figure 6: Vertex Tree

This implementation uses an octree-based Vertex Tree. The octree has the advantage of implicit hierarchical spatial information and can be traversed quite fast. Each node of the Vertex Tree (octree) contains following elements:

class CNode {
    int     Label;
    int     Depth;
    Vector  RepVertex;
    Vector  Center;
    float   Radius;
    list    TriList;
    list    SubTriList;
    Node*   Parent;
    Node*   Children;
}

Label

Indicates the current state of the node. The state can be active, boundary or inactive.

Depth

The depth of the node is used for the efficient generation of the TriList and SubTriList during the generation of the Vertex Tree.

RepVertex

The coordinates of the representative vertex. All vertices inside a node will be collapsed to this representative vertex, if the node is collapsed.

Center

The coordinates of the center of the node.

Radius

The radius of the smallest sphere with center Center, which contains all vertices of the node. The Screenspace Error caused by collapsing this node is calculated from this radius.

  

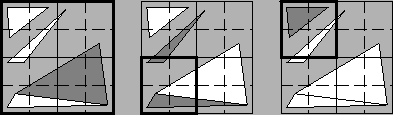
Figure 7: SubTris (dark) of three nodes (bold)

TriList

A list of all triangles, which have exactly one vertex inside the node. The vertices of these triangles will be corrected (to the node's representative vertex), if the node is collapsed. Expanding sets the vertices of the triangles to the representative vertex of the first active ancestor node.

SubTriList

A list of all triangles, which have two or three vertices inside the node, but not more than one vertex in every child node (Figure 7). The second condition ensures that each triangle appears at most once in the SubTriList, if an arbitrary path from root to leaf is considered. Hence, the triangles are removed exactly once from the Active Triangle List when the node is collapsed and are added again if the node is expanded. It is impossible that identical triangles are removed or added several times.

Parent

contains the parent node.

Children

is a list of the child nodes of the node.

The implementation which is the base for this paper uses triangle lists TriList and SubTriList which are dynamic arrays from the C++ Standard Template Library. In contrast to the Active Triangle List, these lists change only during the generation of the Vertex Tree und remain unchanged afterwards. Dynamic arrays are a good compromise between access speed and memory requirement.

Collapse Node and Expand Node

The two fundamental operations on the Vertex Tree can be described as follows:

CNode::collapseNode()
    Label = BOUNDARY;
    foreach child C
        if (C->Label == ACTIVE)
            C->collapseNode()
        C->Label = INACTIVE;
    foreach triangle T in N->TriList
        foreach corner c of {1,2,3}
            T->proxies[c] = firstActiveAncestor(T->corners[c]);
    foreach triangle T in N->SubTriList
        removeTri(T);

CNode::expandNode()
    foreach child C
        C->Label = BOUNDARY;
    Label = ACTIVE;
    foreach triangle T in N->TriList
        foreach corner c of {1,2,3}
            T->proxies[c] = firstActiveAncestor(T->corners[c]);
    foreach triangle T in N->SubTriList
        addTri(T);

Screenspace Error

Generally, arbitrary error metrics can be used by HDS; this implementation uses a Screenspace Error Metric. Consequently the size of each node projected to the picture plane is observed. If the node's size shrinks below an user defined threshold the node will be collapsed and if the node's size exceeds the threshold it will be expanded again. Due to this mechanism smaller respectively distant parts which would be smaller than e.g. 2 pixel on the screen, are not displayed.