Recently Keller[Kel95] proposed the application of quasi-Monte Carlo quadrature[Nie92] for the radiosity problem as a promising alternative to Monte-Carlo or classical integration rules.
For the normalised, s-dimensional integration domain ![]() ,
the quasi-Monte Carlo approximation is:
,
the quasi-Monte Carlo approximation is:
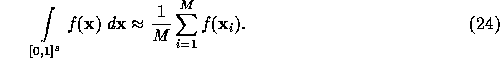
Sample points ![]() should be selected to minimise the error of
the integral quadrature.
should be selected to minimise the error of
the integral quadrature.
If the integrand f has finite variation in the sense of Hardy and Krause, then the error of the quasi-Monte Carlo quadrature can be bounded using the Koksma-Hlawka inequality:
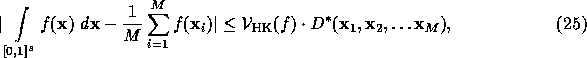
where ![]() is the variation in the sense of Hardy
and Krause and
is the variation in the sense of Hardy
and Krause and ![]() is the star-discrepancy of the sample points[Nie92].
The star-discrepancy -- which is a measure
for the deviation from uniform distribution -- is defined by
is the star-discrepancy of the sample points[Nie92].
The star-discrepancy -- which is a measure
for the deviation from uniform distribution -- is defined by
![]()
where A is an arbitrary s-dimensional subcube parallel to the coordinate axes and originating at the centre, V(A) is its volume, and m(A) is the number of sample points inside this subcube.
For carefully selected sample points, called low-discrepancy
sequences[Nie92], the discrepancy and consequently the error can be in
the order of ![]() , which is much better than the
, which is much better than the ![]() probabilistic error bound of Monte Carlo methods [Se66, Sob91].
Moreover, quasi-Monte Carlo methods guarantee this accuracy in a
deterministic way, unlike Monte Carlo methods where the error
bound is also probabilistic.
probabilistic error bound of Monte Carlo methods [Se66, Sob91].
Moreover, quasi-Monte Carlo methods guarantee this accuracy in a
deterministic way, unlike Monte Carlo methods where the error
bound is also probabilistic.
However, function f that needs to be integrated in rendering problems is usually discontinuous and thus has infinite variation (a function of finite variation can have discontinuities parallel to the coordinate axes only[Deá89]). Although practical experiences show that even for discontinuous functions, quasi-Monte Carlo methods can be better than Monte-Carlo methods[Kel96], their advantages seem to be less than predicted by the theory for functions of finite variation.