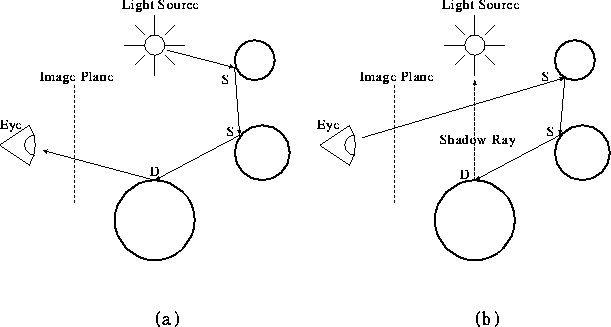
Figure: Classical ray-tracing methods (a: photon tracing, b: visibility ray tracing
Hybrid algorithms combine the classical radiosity and classical ray tracing [Gla95]. These algorithms are usually called multipass methods because typically they are implemented by a sequence of radiosity and ray tracing steps. The hybrid algorithms try to exploit that the strengths and weaknesses of radiosity and ray tracing are complementary.
The classical ray-tracing method is a very simple way of photorealistic rendering, which does not need a meshing or other pre-processing of the scene. Rays are traced backward from the viewpoint through the pixels of the image plane. The colour of the appropriate pixel is computed according to the ray-object interactions.
Strengths of ray tracing:
Weak spots of ray tracing:
Classical radiosity is a finite-element method for solving the rendering equations. This method requires a meshing of the scene, which produces several artefacts. On the other hand, after the radiances of different surface elements (patch) have been computed once the scene can be rendered efficiently from different viewpoints.
Strengths of radiosity:
Weak spots of radiosity:
Heckbert introduced a regular expression formalism which is for describing the chain of ray-object interactions like reflections or refractions etc [Gla95][Hec91]. The different rendering algorithms can be characterised by the group of such regular expressions representing the type of the ray-object interaction sequences which are modelled by the given algorithm. Emission of a photon from a light source is written L, and absorption at the eye (or intersection with the image plane) is written E. Along a way from L to E the photon may be speculary reflected or transmitted (written as S), or diffusely reflected or transmitted (written as D). In the sequence the first letter is L and the last one is E, and standard computer-science regular expressions can be used between them. Subexpressions may be grouped in parentheses, an asterisk superscript * represents 0 or more repetitions. A term in square brackets is optional (it may be included or not).
Classical ray tracing only models specular reflections and transmissions (both represented by the letter S), so it can be described as modelling L[D]S*E paths. This characteristic expression can generate four different types of strings, representing the different light paths that can be captured by classical ray-tracing model: LE, LDE, LS*E and LDS*E. After reaching a diffuse surface only the direct illumination is gathered at this point, so classical ray tracing does not model the multiple diffuse reflections or refractions.

Ray tracing has two alternatives photon tracing and visibility ray tracing [Gla95]. In photon tracing (forward tracing) the rays are emitted from the light sources while in visibility ray tracing (backward tracing) rays are emitted from the viewpoint. In both methods rays are traced until they reach a diffuse surface (unless they leave the environment), so child rays are only generated (and traced recursively) when the given ray hits a specular surface. The main difference between these two alternatives is that visibility tracing models paths L[D]S*E and photon tracing models paths LS*[D][E]. In the second case the E is optional because paths do not necessary end at the eye.
The combination of photon tracing and visibility ray tracing is called bi-directional ray tracing, because rays are traced in both directions [Gla95][Arv86][CF87][Hec91]. Bi-directional ray-tracing algorithms model the paths LS*[D]S*E. This is not quite the full range of possible expressions, but it is more then either algorithm can produce alone.
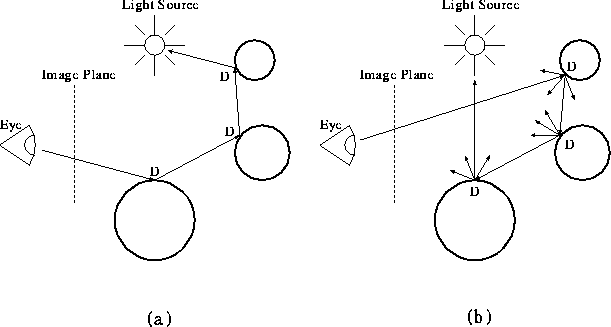
Distributed ray tracing suggested by Cook [CPC84] can in theory model all the possible paths represented by L(S|D)*E. In this method the tracing of rays is not terminated reaching a diffuse surface. For modelling multiple diffuse reflection and refraction the Monte Carlo techniques are used. After a ray has hit a diffuse surface child rays are generated randomly according to the BRDF (bi-directional reflection/refraction distribution function) characterising the surface. For appropriate estimation of multiple diffuse illumination several child rays have to be traced computing the average of their contributions. This approach is the direct use of Monte Carlo technique, since it samples the signal represented by incident light on the shading point.
Another Monte Carlo approach proposed by Kajiya is path tracing [Kaj86]. This method simply creates a path history for a single particle interacting with the environment until absorption. That is, rather than spawn new rays at an intersection, we simply choose a random direction according to the BRDF for the one ray to follow.
In the following, ray-tracing methods are reviewed which are based on the Monte Carlo or quasi-Monte Carlo integration techniques.