Monte Carlo Light Tracing

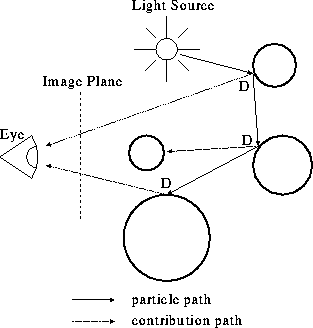
Dutre proposed an algorithm that does not require mesh generation and can handle all types of light-surface interactions [DLW93]. This algorithm is based on particle model and direct computation of pixel intensities. Particles perform random walk through the scene and whenever a surface is hit, a ray is traced from the intersection point to the eye and direct light source contribution is added to the relevant pixel.

The random walks are denoted by a sequence of pairs , where and is the last point generated. For the ith particle the pair is the pair representing the starting point and starting direction of the ith particle.

 
for each particle (  ):
	determine the starting position   
	trace a ray towards the eye and add the direct light source
	contribution to the relevant pixel
	determine the new direction   
	absorbed = False;   
	repeat until absorbed:
	  	compute   
		trace a ray from    to the eye and add the reflection
		contribution to the relevant pixel
		use the subcritical PDF to generate    or
		to absorb the particle
		j=j+1
determine    for each pixel
display image

Figure: Particle tracing

The new direction is chosen according to the subcritical pdf (spdf) on the basis of importance sampling:

where is the bi-directional reflection distribution function (BRDF). The pdf is subcritical because it does not integrate to 1 over all possible angles, at least for physically valid BRDFs. The actual value of the integration gives the chance that random walk is continued, which ensures that the random walk terminates. This technique is commonly called Russian roulette.