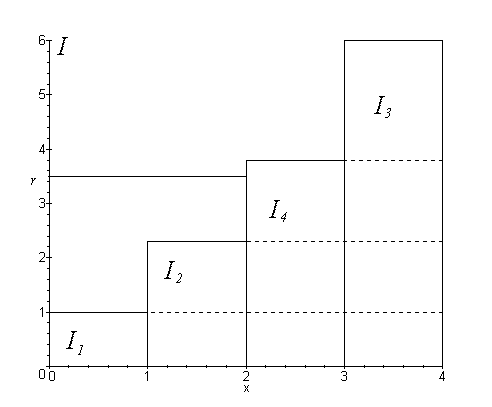Importance Sampling Using Particle Distribution

Particle Tracing Methods in Photorealistic Image Synthesis
Rázsó István Márk
rezso@inf.bme.hu
Department of Control Engineering and Information Technology
Technical University of Budapest
Budapest, Hungary

Next:Our work Up:Contents Previous:Mesh generators

An importance sampling technique using the particle distribution

To evaluate the rendering equation, Monte Carlo integration techniques can be used. In these methods we sample the integrand at random directions. Random sampling is very inefficient, because we have a very small chance to pick a direction where significant amount of light can come from. It would be a good idea to sample the integrand from directions contributing most of the outgoing radiance, so another algorithm, importance sampling can be used. The basic idea behind importance sampling is to place more samples where the integrand function is larger. The sampling can be described with:

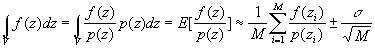where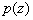

is a probability density in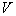

, the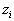

points are selected according to this probability density, and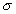

is the variance. The variance can be minimized if

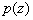is proportional to the integrand

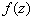A path tracer works in the following way: we generate a starting direction from the camera. We examine whether a surface is hit or the particle leaves the scene. If a surface has been hit, we generate a new direction. In case of importance sampling this new direction depends on some kind of knowledge about important directions. We continue this process until a lightsource has been reached or the photon leaves the scene. At each reflection point we have to scale the calculated radiance according to the probability distribution of the importances.
If we examine the rendering eqation:

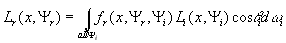we can see that an impotance sampling algorithm can use the physical characteristic of the surface (its BRDF) to generate the important directions. With the outgoing direction and the BRDF we can select the incoming directions which carries most of the radiance. This algorithm does not need to have knowledge about the global illumination at the surface, which is also part of the rendering eqation.
We can use the particle data to drive an importance sampler in a path tracer algorithm. For this algorithm the important properties of a particle are its power, its position in the scene and its incoming direction.

How to generate important directions

We are interested in generating directions which contribute most of the outgoing radiance at . We estimate the incoming radiance using the generated particle distribution in the scene. This importance sampling technique is presented in [5]. At a surface point we construct a hemisphere or a sphere (if the surface is diffusely transparent) which will describe the important sampling directions. We build this importance map by the following algorithm:

Initialise the (hemi)sphere to zero in each region
Find the N nearest neighbour of the point currently hit. This N is a fixed number during the algorithm.
Assume that each neighbour has been reflected at 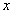. For each neighbour, calculate the product of the incoming power of the particle and the BRDF. The BRDF is evaluated in the direction of the sampling ray, and the direction of the incoming particle.
Add this value to the region which contains the particle’s incoming direction.
When every particle’s contribution is added to the sphere, distribute a small portion of the total importance in the sphere among each region. This operation is important, because only this way can the algorithm generate sampling rays in directions where no particle came from.
Generate a new sampling direction.
Scale the returned radiance. Because importance sampling is used, we have to scale the radiance returned by the sampling ray. The scaling factor is:

Figure 5 shows a hemisphere, and an importance map. To decide how many regions should an importance map have, we have to run simulations, and measure the quality of the images and the computation times.

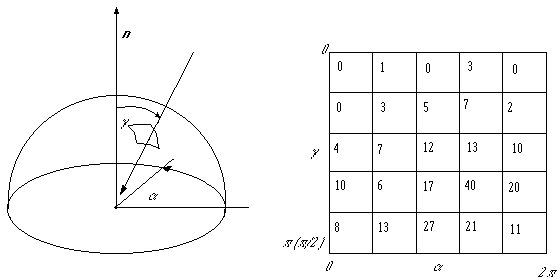
Figure 5: Left: a hemisphere with an incoming photon direction. Right: an importance map

To generate an outgoing sampling direction, we have two possibilities. The first method is based on mip-mapping. We demonstrate this algorithm in a case where we have just four areas with importances I1, I2, I3 and I4. This transformation decomposes a rectangle of size A x B to four subrectangles having an area proportional to the importances of the original rectangles. Then we generate a uniformly distributed random point in the transformed rectangle. We find the original rectangle for this point and scale it’s coordinates to represent a point in the original rectangle. Figure 6 illustrates this method.

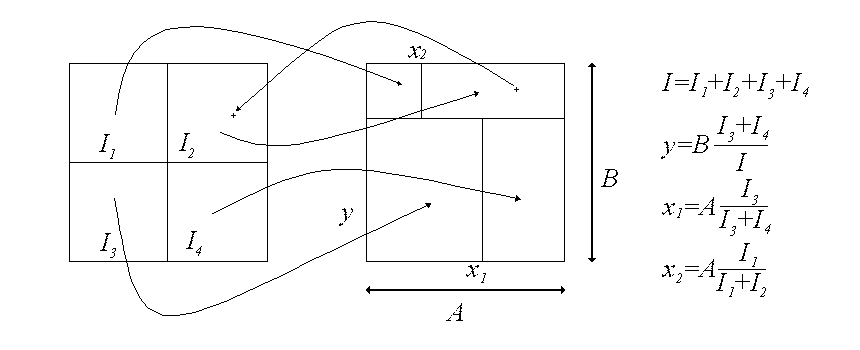
Figure 6: The mip-map based generation of a sampling direction

The second method is a kind of a linear inversion technique. This method takes advantage of the fact that the inportance map is discretized, thus it can be considered as a one-dimensional, row continous array. The algorithm selects an element of this array proportional to its importance. We sum all the importance weights of the areas and generate a random number in the range of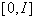

, where I is the sum. Then we scan the rows of the importance map and sum up the importance values. When this sum becomes greater than the generated random number, we select the last region whose weight was added to the sum. Then we can generate a random point in the selected region. Figure 7 shows how this algorithm works.

Figure 7: Selecting a region with random number .