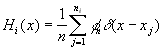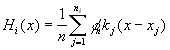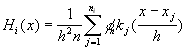Mesh Generators

Particle Tracing Methods in Photorealistic Image Synthesis
Rázsó István Márk
rezso@inf.bme.hu
Department of Control Engineering and Information Technology
Technical University of Budapest
Budapest, Hungary

Next:Importance Sampling Up:Contents Previous:Introduction

Mesh generator algorithms

In these type of algorithms we use the previously generated hit points on the surfaces with an associated incoming power. For these algorithms we must store the power of the particle, the surface which the particle hit and a local coordinate on the same surface.
We are interested in the diffuse radiance of a surface. A Lambertian surface has a constant BRDF ( ) for all incoming/outgoing directions, where is the reflectance. This implies, that a Lambertian surface will have a constant surface radiance for all incoming/outgoing direction pairs. On a Lambertian surface at coordinates, we have a surface reflectance and an irradiance . The radiant exitance of the surface at is . The radiance is , or it can be expressed like . This equation implies that we can store the irradiance and the reflectance of the surface independently, and later reconstruct the radiance.
At this point, we have to generate surface meshes from the irradiance presented by the photon hits. This is a density estimation problem, where we have non-uniform random samples. To estimate this photon density, there are different classes of density estimation algorithms have been used:

Histogram methods: The surface is subdivided into buckets in which the number of photons and/or their accumulated energy is stored.
Nearest neighbour methods: The density at a point is estimated by dividing the power of the nearest N neighbours (usually it is a fixed number) by the area of a region (centered at the point) containing these photons.
Kernel estimators: The density is estimated as spatially spread energy distributions.

Figure 3 illustrates these three different types of estimation techniques.

Figure 3: Different methods to estimate the irradiation at X from the distribution of the photon hits. On the left: Histogram technique, in the middle: the nearest neighbour method, on the right: there are few photons with their kernels, shown from above.
Kernel estimators

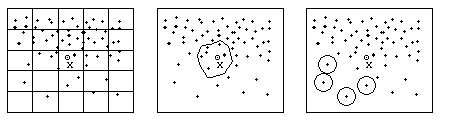
We have a list of hit points for each surface, and we have to estimate the irradiance on the surface. The irradiance is represented by these hits, where a finite amount of energy strikes an infinitely small area. In one dimension the density function of the irradiance can be represented by taking samples ( ):

where

is the power of the

th photon. We know that the irradiance is a smooth function, so to place a spike at every photon hit would not be a good idea. Instead we use smooth kernel functions and replace the delta functions with

, where

has a unit volume. A kernel function spreads the energy of the photon over its surrounding area. These kernels should be centered at the origin, have a non-zero region, and be "lump" shaped. Figure 4 shows an example for a two dimensional kernel function.

In two dimension, the irradiance function can be estimated:

where

is the position of the

th point. If we replace the delta functions with

kernel functions

The kernel functions have the conflicting requirements of being narrow enough to capture detail, and wide enough to eliminate the randomness caused by the non-uniform sampling presented by the hit points. We can use a scaling parameter

to widen or narrow the filter. We have to preserve the volume of the kernels, so we increase the height:

Examples for kernel functions can be found in [1], [2].
To generate meshes from the estimated irradiance, we can sample

at a finite set of locations and use some polinomial elements to interpolate between these values. We can use these polinoms during rendering, or we can generate meshes for the surfaces describing the irradiance.