Interpolation CT slices

Reconstruction of Tomographic Data by Markov Random Fields
Marek Zimanyi

Department of Computer Graphics and Image Processing
Comenius University
Bratislava, Slovakia

Abstract

The most important part of 3D visualization of tomographic data is an object model reconstruction. The traditional reconstruction techniques include some artefacts since the distances between slices are too big. We cannot scan the CT slices of smaller distance due to either the radiation dose or the time.We have developed a new statistical reconstruction technique based on both data modelling by Markov random fields and finding solution by Simulated annealing algorithm.

Proposed technique:

Introduction

Modeling data object by Markov Random Fields

Optimalization

Information about CT scanner

Introduction

    CT scanner provides an information about scanned object, which is put in set of 2D projections-two dimensional pictures, slices. This slices are saved in a digital form and ready for other use.
    Visualization is a very important part of CT slices processing. This scanned data visualization might be based on simple display of single pictures or on a more difficult reconstruction of a 3D object model. We are particularly interested in this second part of the CT slices visualization.
    Traditional interpolation techniques contain many different artifacts (postaliasing, prealiasing, ringing ...), which arise while scanning an object (noise) or during the reconstruction itself. This artifacts depend on the size of interval the object was scanned within. It was a reason which led us towards the idea of creating a new reconstruction technique. This technique suppresses previously mentioned artifacts and uses parameters obtained from CT scanner.
    The main goal of our work is to introduce a new statistical reconstruction technique which uses both Bayesian paradigm and data modelling by Markov Random Fields (MRF) tomographic data processing. A new consequential model is created according to the qualities of CT scanner and scanned data. Our program interpolates data with this new technique.
    We transform the reconstruction problem of 3D object to the 1D object reconstruction. This 1D object is a perpendicular line on slices ( figure 1a ). A value of any pixel of this line is a value of the function in this point (figure 1b, c).

Figure 1. Top

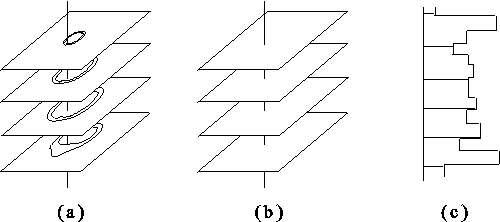
Modeling data object by Markov Random Fields

We express relationship between scanned data and the set of values f by Bayes formula [Li]:

p( f / d ) … conditional probability of data model f given the measured data d. Its maximalization gives solution f*=arg_max p(f/d).
p( d / f ) … This probability we obtain from simulation scanning of tomograph on model f .
p( f ) ……. A priori information about the object, obtained independly of the results of the measurment. It will be derived from the assumption of MRF model.
p( d ) …… Probability of the single realization measured data. It will be constant.

p(d / f):
If we assume Gaussian noise, we can express probability p(d / f) as

where

,

fct_i are sampled model f by simulation of tomograph (convolution with gaussian, see Parameters of CT scanner).

p(f):
From Markov random fields theory we can express a priori probability p(f) as

where

V_c(f) is a set of potencials of model f .

p(f / d):
Since p( d ) is fixed for " f Î L (set of all values model f , 256 level of greyscale) we can express solution f*as

From p( d / f ) : p( d / f ) = Z₁´e^-U(d/f)and from p( f ): p( f ) = Z₂´e^-U(f) where Z₁and Z₂ are constants we obtain

Since a generic constraint is smoothness (express by derivations,

) we get

where g( f' ) can be replaced by (| f' |) or (| f' |-ln(1+f'²)). For more information how we obtain g( f' ) see framework Statistical interpolation.
Now we can find a solution by simulated annealing, where f is modeled by MRF aproach.

Top

Optimalization

    We use Simulated Annealing (SA) [Li] for minimalization of the energy E(f). SA simulates the physical annealing procedure in which a physical substance is melted and then slowly cooled in a search of a low energy configuration. For the escape from the local minimum to the global minimum the Metropolis algorithm is used. At each step the following configuration f' is randomly chosen from N(f) ( the vicinity of f ), for instance, by changing one of the f_i's into a new label f_i'.

    Metropolis:
            initialize f,
            repeat
                generate f' Î N(f);
                DE ¬ E(f') - E(f);
                P = min{1, e^-DE/T};
                if random á0,1) < P then F ¬ f';
            until (equilibrium is reached)
            return f

SA applies a sampling algorithm, Metropolis, successively at the decreasing values of the temperature T. The starting temperature is choosen from Metropolis algorithm: T is the start temperature when number of accepted statuses is 70 - 80%. Number of iterations we can choose 10n or 5n, where n is a number of sites. The decreasing sequence of temporary must satisfy lim_{t -> µ} T^(t)=0. So T^(t) we can choose as T^(t)=(C / ln(1+ t)) or T^(t) = kT^(t-1).

    Simulated Annealing:
        initialize T=T_max and generate f
        repeat
            Metropolis(T,f);
            decrease T;
        until (T > Tmin)
        return f

Top

Information about CT scanner

The parameters of CT scanner are thickness and radiation intensity. We can express these parameters by the Point Spread Function (PSF). The x axis is perpendicular on CT slice and axis y is paraller to it. Scanned material is a plate with the thickness w and with the inclination 45^o according to the plain of scanning. y axis goes through the slice and x axe is perpendicular on y, and goes through the first intersection of the material with y axis.

We examine an intensity of scanned point in y₀.

Figure 2 The value in point y₀ is

where h(x) is PSF and g(x,y₀) are values of scanned material.

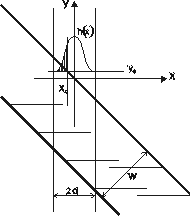
But the function f(y) on interval <-d,d> is discrete and so we can substitute f(y) by the set of values f={ f₀, f₁, ... , f_m}. Then h_i= (f_i- f_i-1 )/d_i, where d_i is a distance between neighbor points.

We choose an approximate function (e.g. Gaussian) from these points or we use directly these points.

References

Top

Download this paper