Issues on Displaying 3D Data for Scientific Visualization Thomas Theußl theussl@cg.tuwien.ac.at Institute of Computer Graphics Vienna University of Technology Vienna, Austria

Stream Arrows

In Section 2 several approaches were discussed which try to visualize three-dimensional flow by depicting lines in space. Another approach would be to visualize dynamical systems by depicting stream surfaces. A major problem thereby is that such surfaces often occlude major parts of the model. Again, transparency alone does not solve the problem for transparent surfaces provide little depth cues. Furthermore, since flow has a direction it would be desirable to visualize this direction too.
An extension to standard stream surfaces that on the one hand lets one see through the surfaces and on the other hand depicts the direction of the flow is the use of stream arrows [10]. Therefore, arrow-shaped textures are mapped to the surface, which both depict the direction of the flow and can be made transparent to show what lies behind them (however, it is also possible to make the remaining surface transparent and depict the stream arrows opaquely). Figure 9 shows a stream surface with stream arrows which, since they are transparent, let one clearly see the inner structure of the dynamical system.
The problem with this approach is that the arrows are equal-sized in texture-space so they tend to become too big or too small in areas where stream surfaces spread over regions of high divergence or convergence. To generate stream arrows that are almost equal-sized in the final image it is better to use hierarchical stream arrows [9]. Therefore, a stack of stream arrows textures is defined, where the scale relation of the arrows between successive levels is defined by a constant factor. The ratio between the size of a mesh in texture space and in phase space is then used to find the most appropriate level in the stack, which makes the arrows almost equal-sized in the rendered picture. It would not be useful to define a continuous size function for this purpose because the ability to represent local divergence or convergence would be lost then.

  
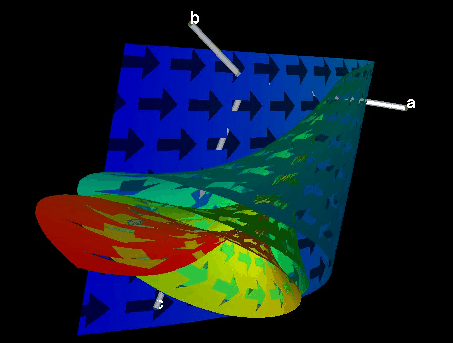
Figure 9: Stream arrows on a stream surface of a dynamical system.