|
[initial patch]
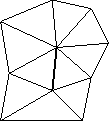 [edge collapse]
[edge collapse]
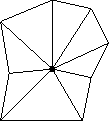 [edge split]
[edge split]
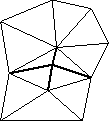 [edge swap]
[edge swap]
|
Although the approach in [9] is not immediately related to multiresolution, it introduces some concepts HOPPE'S further work is based on. The primary goal of this paper is to approximate surfaces reconstructed from unorganized points. Therefore the input data is assumed to be a set of points rather than a continuous surface.
The tradeoff between the number of vertices and the approximation quality is defined by an energy function. Thus large geometric errors are penalized as well as a large number of vertices, where the relative weight between these contradictory goals is defined by the user. The optimization procedure tries to find the mesh with minimum energy.
Optimization is performed by two nested loops. The outer loop modifies the mesh connectivity by randomly selecting an edge and performing one of three possible edge operations (collapse, split, and swap, see figure
|
[initial patch]
 [edge collapse]
[edge collapse]
 [edge split]
[edge split]
 [edge swap]
[edge swap]

|