Progressive Meshes

The results explained in the previous section are extended in [5] to define a multiresolution representation called Progressive Meshes (PM). It is constructed by iteratively applying the edge collapse operation to the input mesh until some error threshold or a specified number of faces is reached. The edges are no longer selected at random. Instead they are taken from the head of a priority queue sorted by increasing error introduced by the collapsing operation. Therefore the mesh is a good approximation at each step (not only at the end of simplification). When no more edge collapse operations are performed, the resulting mesh (the base mesh) is stored together with a sequence of split records as the PM representation. The vertex split operations are the inverse of the corresponding edge collapse operations (see figure

Figure 3: Different definitions of the mesh operations vsplit and ecol

[according to [5]] [according to [6]]

(0,0)(0,0)

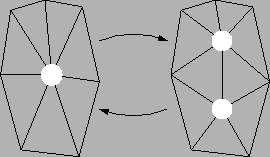
(32,90)(0,0)v_s

(82,128)(0,0)vsplit

(84,54)(0,0)ecol

(138,112)(0,0)v_t

(138,69)(0,0)v_s

(127,90)(0,0)f_l

(149,90)(0,0)f_r

(-8,90)(0,0)v_l

(69,85)(0,0)v_r

(99,90)(0,0)v_l

(176,85)(0,0)v_r

(235,90)(0,0)v_s

(218,78)(0,0)f_n0

(218,100)(0,0)f_n1

(252,77)(0,0)f_n2

(252,100)(0,0)f_n3

(285,128)(0,0)vsplit

(287,54)(0,0)ecol

(341,112)(0,0)v_u

(341,69)(0,0)v_t

(325,69)(0,0)f_n0

(325,113)(0,0)f_n1

(356,66)(0,0)f_n2

(356,113)(0,0)f_n3

(330,90)(0,0)f_l

(352,90)(0,0)f_r

3(a)).

The PM representation is also able to take into account attributes such as color and normal vectors. Furthermore discontinuity curves defined as abrupt changes in these attributes between adjacent faces are considered. Avoiding modifications of the topology of discontinuity curves improves the appearance of the simplified mesh. The energy function (see section 3.1) is extended two deal with these two concerns.